爱因斯坦相对论论文分析进展

经过一天的折腾，连蒙带猜，终于弄明白了爱因斯坦的思路。虽然他写作非常不清晰，变量名混淆扰乱思路，各种动机不明，逻辑混乱，但最终的问题终于被看出来了。

爱因斯坦的公式推导里面其实有一个隐含的，未经实验证实的假设，那就是光的相对速度对于任何运动中的观测者都是一样的，都是 c。注意，这个假设说的不是通常所谓的“光速不变”。通常说的“光速不变”，只是说光速不随“光源”的运动而改变，并没说光的相对速度不以“观测者”的运动而改变。注意这两者的差别，一个是说光的发出者，一个是说光的接收者，完全是两回事。前者我可以接受，但是这后者其实是未经实验证实的。

爱因斯坦在第一节提出“前提”的时候，只说“光速不变”的意思是光速不随“光源”（原文叫“emitting body”）的运动而改变，可是到后来，他其实假定了光的相对速度不随“观测者”的运动而改变，却始终没有明确的把它提出来说清楚。这导致他的公式推导，各种操作的动机非常难以理解。

只是在下面讨论“同步”的时候，他通过“定义”（by definition）的方式，假设光“从 A 到 B”和“从 B 到 A”需要的时间是一样的。注意这只是一个“定义”，不是一个已经被实验证明的事实。这个“定义”其实隐含了“光相对于任何运动的观察者的速度都一样”，但是他始终没有强调这个重要的前提，只是在后面突然开始使用它。

一般的物体，当观察者运动的时候，物体相对于观察者的“相对速度”是会变化的，但这个假设说光是一个例外。不管观察者如何运动，他测出来的“光相对于自己的速度”都是一样的，仍然是 c。

这是什么意思呢？我举一个例子。假设你以接近光速的速度（比如 c-1 m/s）在运动，只比光速慢了 1 m/s。这时候背后有一束光追上来。因为你的速度很快，所以这束光花了很长时间，一米一米地接近你。60 米的差距，这束光花了一分钟才追上你。你测了一下光的速度（如果能测的话），发现这束光相对于你的速度是 c。你觉得这有可能吗？如果你觉得这例子还不够，再想一下，要是这时候迎面也来了一束光，你测出它相对你的速度也是 c。这不奇怪吗？

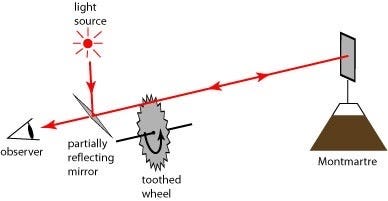
“光的相对速度不随观测者的运动而改变”，这个说法其实是没有经过实验证实的。为什么我这么说呢？因为所有测光速（或者变相测光速）的装置，包括 Michelson-Morley 实验在内，里面的光都是“往返”运动的，从来不是“单程”。他们测的都不是瞬时速度，而是往返总路程的平均速度。他们总会放一个镜子在那里，把光射过去，再反射回来，计算总路程和时间，然后用“路程/时间”算出平均速度（如图）。

参考这个视频，你会发现从来没有人测过“单程”或者“瞬时”的光速，全都是在测“往返”的平均光速。

稍微思考一下就会发现，如果整个测光速的装置都在运动中的话，这样的“往返”路程算出来的平均速度，是无法反映每段路程的“相对速度”的。比如装置以 v 的速度朝着光发出的方向在运动，那么“光相对于接收器的速度”，去的时候是 c-v，回来的时候是 c+v。但因为镜子和接收器同步在动，相对距离不变，所以光经过的总路程和时间都不随 v 改变。最后你用这些数据算出来，就以为光的相对速度一直是 c 没变过。而其实它的相对速度过去的时候慢了一些，回来的时候快了一些。

你不知道是这样，因为你没测过单程光速，也没测过光的瞬时速度。诚然，测量单程光速和光的瞬时速度是很难的，但你不能因为实验有难度，就假定“光的相对速度不随观察者的速度而改变”，然后用数学推导出一大堆奇怪的理论来。这不是科学的做法。

但爱因斯坦的论文就是基于这么一个假设，然后列出一些等式，刻意把时钟调了一下，让你用这些时钟算出来的光速总是 c，就算是单程的也一样。被这样的数学一搞，时间当然就只有“膨胀”了（time dilation），但这真的反映了物理的现实吗？把一个未经实验证实的假设直接放进数学公式求解，不管解出来的东西是什么，就认为那是现实，或者拿出一些模棱两可，难以核实的“证据”来。这不叫物理。

具体的数学计算里面也许还有其他问题，导致他的公式与运动的方向无关，这样就导致了 twin paradox 等悖论的产生。还有 Herbert Dingle 的那个问题，两个互为匀速运动的物体，相对速度是 v，你该把哪一个的速度代进去做变换呢，哪一个的钟该走得慢一些呢？

他的具体数学计算是否有错，还在进一步分析中。