相对光速的误解

看了两个关于“相对光速”的问答（问答1，问答2），发现绝大部分人都认为“光相对于任何观察者的速度都是一样的，永远都是 c”。但他们只是在鹦鹉学舌，显示自己“懂科学”，却从未想过这个说法是怎么来的。

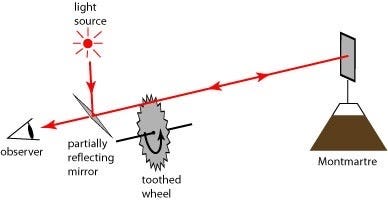
其实这个被世人所接受的“光相对于任何物体的速度总是 c”的说法，只是根据那些“测光速”的实验来的。这些实验者发现，无论测光速的装置以什么速度移动，朝着什么方向，测出来的“光速”总是 c。但这些装置总是用一些镜子，把光原路反射回去，然后用“往返总路程 / 总时间”得到速度。所以它们测的全都是“往返平均光速”，不是“瞬时光速”，也不是“单程光速”。从来没有人测量过“瞬时光速”或“单程光速”。

“速度”这个概念，本来应该是指“瞬时速度”，“瞬时”也包含了“单程”的意思。只有在测“瞬时速度”有困难的时候，才会去测长距离的“单程平均速度”。只有在测“单程平均速度”都有困难的时候，才会去测“往返平均速度”。光就是最后这种情况，因为它跑得太快了，所以测“瞬时速度”和“单程平均速度”都有困难。按照目前的技术水平，就只能测“往返平均速度”了。但是有技术困难不等于你就可以认为“光速”在整个宇宙中相对于任何观察者都是那个“往返平均光速”，把它作为真理教给所有人，并且由它推导出一大堆奇怪的理论来。

“往返平均光速”在一般情况下是可以用的，光相对于空间的速度可能确实是不变的 c，这个速度确实不随“光源”的运动而变化。但谈到光相对于“观察者”的速度（相对光速）的时候，“往返平均速度”就不能用了。顾名思义，光的“相对速度”应该是单方向的光相对于观察者的速度。如果它往返了，“相对速度”这个词就失去了意义，因为相对速度在往返两个方向上可以是不一样的。

一个简单的初中物理练习就可以说明问题。试想你对着墙打网球，假设球相对于地面的速度往返都是 v1。你一边打球一边以 v2 的速度往前走，现在你想知道球相对于你的速度。

分析：由于你在往前走，所以球过去的时候和回来的时候，相对于你的速度是不同的，去的时候是 v1-v2，回来的时候是 v1+v2。但如果你计算球的“往返平均速度”（球往返的路程/总时间），是不可能算出两段路程的相对速度的，你只能得到一个平均速度 v1。走路的速度 v2 因为在往返两段路程是反号的，抵消掉了。所以你不能靠这个计算“往返平均速度”的方法算出球相对于你的速度。要想得到相对速度，你只能测“单程速度”。

这也就是为什么你不能用测“往返平均光速”的装置来测量光的相对速度。如果测量装置以 v 的速度与光同方向运动，那么光相对于装置的速度可能和打球的情况类似，过去的时候是 c-v，反射回来的时候是 c+v，但因为测的是往返平均速度，所以平均下来就是 c。他们就因此认为光相对于任何观察者的速度总是 c，无论观察者如何运动。这是错误的，因为这样测出来的不是光的相对速度，相对速度必须是单程速度。

我觉得大家都太相信这些实验设备了，盲目地以为设备测出来就是对的，却忘记了“相对速度”本来的含义，以至于没有发现这些设备测出来的根本不是相对光速。

然而，就算这些实验没能证明“相对光速总是 c”，它们也没有否决它。如果相对光速总是 c，那么你测出来的“往返平均光速”肯定也是 c，也没矛盾。所以“相对光速总是 c”还是有可能的，只是它没有被实验证明，而且违反经验和直觉。不过我有一个简单的思维实验，也许能说明“相对光速”应该不会总是 c：

假设从 1 光年以外的星球上发出来一束光，同时你坐着飞船以 0.5c 的速度朝着那个星球前进。请问你会在什么时候看到这束光？

这个基础的初中物理题，体现了“相对速度”本来的意义，只不过这里其中一个物体是光。如果照他们说的，无论你的速度是多少，光相对于你的速度总是 c，因为距离是 1 光年，那么你应该在恰好 1 年后看到这束光。就算你加速到 0.9c，或者停下来不走了，或者以 0.9c 的速度朝着反方向前进，你还是会在恰好 1 年后看到这束光，就因为我们相信“光速相对于你的速度永远是 c”。你不觉得这违反了基本的常识吗？